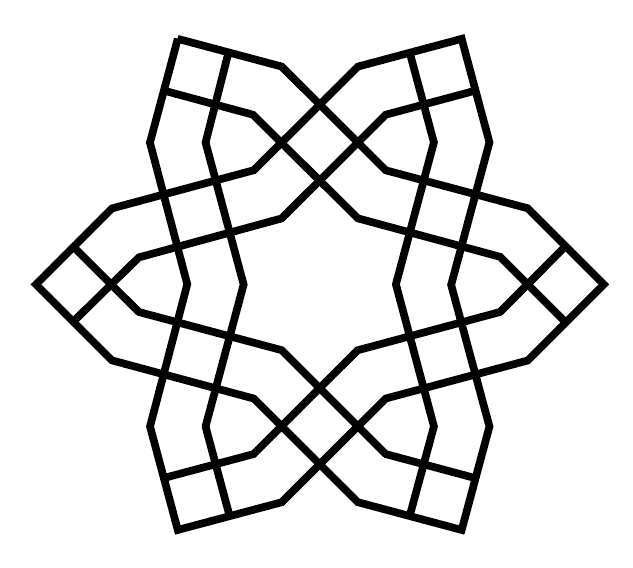
This week, we’re tackling a six-fold star patterns that shows up in Islamic monuments across the world, from the 9th century Mosque of Ibn Tulun in Egypt to the 15th century Shakh-i-Zindeh complex in Uzbekistan and the Eski Mosque in Turkey.
Once you’ve figured out a few geometric basics, you’re ready to learn all about pathways: those lines that go over and under each other to create a three-dimensional effect.
Drawing pathways is a labor of love, but – to me – worth the extra work when you’re playing with a design and want to emphasize the lines rather than the shapes.
Continue readingA friend recently shared a picture with me from a visit they made to The Alhambra in Granada, Spain, a few years ago.
After playing with it for a few hours, I fell in love with this deceptively-simple rosette.
You are no doubt an excellent constructor of four- and six-folded bases by now. It’s time to move on to something just a bit trickier: five-fold patterns. Constructing a five-fold base can be infuriating, but with a little practice, you’ll figure it out in no time. Don’t
You’ll notice that the instructions here are repetitive up until a point; this is so that anyone can start on this page without having to reference anything else.
Continue readingNow that you’ve learned how to make a six-fold model, you’re just a few steps away from turning your mother circle into a four-fold foundation. Four-fold patterns often contain shapes like squares, diamonds, octagons, and wonky forms with curvy lines.
You’ll notice that the instructions here are repetitive up until a point; this is so that anyone can start on this page without having to reference anything else.
Continue readingIf you’ve liked diving into Islamic geometric patterns, it’s helpful to take a step back and look at the underlying armature before going further. Today, we’re going to talk about how to construct six-fold divisions of a circle. It’s called six-fold because it has six mirror lines. To put it another way, if drawn on paper, this pattern could be folded six different ways to create symmetrical halves.
Six-fold patterns will often contain triangles, hexagons, and dodecagons, since 3, 6, and 12 are divisions and multiples of 6.
Continue reading
Since we started with the first geometric pattern that I learned, I thought we’d jump right on over to the most recently one I’ve draw. This pattern is from a window grille in the Mosque of Ibn Tulun, the oldest mosque in Egypt and the oldest surviving mosque in Africa. We drew this with William Charles Riding and the Prince Foundation School of Traditional Arts.
It’s also another a six-fold pattern with a central star. This time, though, the angles in the star aren’t 60º, so it requires a few extra lines.
Mamoot 